Apologies if this is not the clearest post ever. It's just that I finally put together a few loose ends that were bothering me about the two-slit experiment, and I want to record them.
First, some "basic" QM, from Richard Feynman:
A simple example will help here.
Now we want to know: what is the probability of a particle in state |a> being measured in state |b>?
This is just classical probability theory. It turns out that if we do try to detect which way the particle went (i.e., measure it in the x-y basis, followed by the a-b basis), we find it ends up in |b> half the time.
But QM predicts that |a> should never be measured as |b>, because they're orthogonal. What went wrong is that we cannot assume that it went through either |x> or |y>.
|a> = 1/√2(1, i)
|b> = 1/√2(1, -i)
<a|b> = 1/√2 (1 * 1 + -i * -i ) = 1/√2 (1 - 1) = 0
The terms in the above sum are the terms in Feynman's (2). We could have also written this as
(Because <x|a> is just the x-component of |a>, and <a|x> is its conjugate). Sometimes you see this written:

Where i takes on the basis vectors under consideration (in this case, x and y), and:
If you compare the two calculations (for the classical, or "which-way" case, vs the quantum case), you'll notice that they differ by some terms that we can call "interference terms." There's nothing really interfering here, unless we force ourselves to think of |a> and |b> in terms of the x-y basis, in which case we can understand this as the |x> and |y> components interfering.
Elsewhere I've demonstrated why entangling a state |x> + |y> (so that it results in |x>|0> + |y>|1>), results in a similar loss of interference (and I give a quick rehash at the bottom).
Anyway, that was all a prelude to the main course: what's happening in the two-slit experiment?
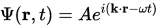
Ignoring the time component, we see that it's basically a complex number whose phase is proportional to r, which is the distance from the source. In our case we're actually close to the source, and the light's strength will be proportional to the inverse of the distance squared.
(One super confusing thing is that in some contexts, the whole Ae^(i*t) is called the "complex amplitude," but in other contexts, we call just A the amplitude. Let's not do the second. Another super confusing thing is that often when referring to the "phase" of a photon, we're talking about the relative phase of the polarization components.)
For any given point on the screen, we will have one such complex amplitude for each slit. Per Feynman's (2), we can just sum these to get the overall amplitude that will give us the probability of finding a photon at that point.
It's hard to get an intuition for what this sum looks like without pictures, but basically you're getting two complex numbers that are sometimes "in phase" (i.e., sum to a number whose modulus is bigger) and sometimes "out of phase" (mostly or entirely cancel). The overall pattern is the one you've seen before:
If we know which way the particle went, we use (3). It's hard to say the "reason" that we use that formula, but again, if we look at knowing which-way as just an entanglement rather than a "collapse" (thereby preserving the quantum nature), it turns out that equation (2) does just reduce to equation (3).
|a> = |x> + |y>
|b> = |x> - |y>
Suppose Pb is the projector onto state |b>, which gives us the probability that some state is measured as |b>. Notice that Pb(|a>) = 0-vector. But now let's entangle it:
|a'> = |x>|x> + |y>|y>
To find the probability that |a'> ends up in |b>, we can't use Pb (since it operates on C2, whereas we now need a projector on C2⊗C2). Instead, we use Pb' = Pb ⊗ I.
If you look at the action of Pb' on |a'>, you will discover that it is not the zero-vector, but instead
√2/4 (|x> - |y>)⊗(|x> - |y>)
whose norm-squared is 0.5, just like we saw in the classical case above.
Another way of seeing this is simply writing |a'> in the a-b basis, and noticing that half of it is in |a> and the other half in |b>:
|a'> = (|a> + |b>)(|x>) + (|a> - |b>)(|y>)
= (|a>)(|x> + |y>) + (|b>)(|x> - |y>)
= |a>|a> + |b>|b>
Whew.
First, some "basic" QM, from Richard Feynman:
1. The probability of an event is given by the square of the absolute value of a complex number φ which is called the probability amplitude:
P = Probability
φ = probability amplitude
P = |φ|2
2. When an event can occur in several alternative ways, the probability amplitude for the event is the sum of the probability amplitudes for each way considered separately. There is interference:
φ = φ1 + φ2
P = |φ1 + φ2|2
3. If an experiment is performed which is capable of determining whether one or another alternative is actually taken, the probability of the event is the sum of the probabilities of each alternative. The interference is lost:
P = P1 + P2
A simple example will help here.
Consider vectors in C2
Consider a basis {x, y} and alternate basis {a, b} where:
a = 1/√2(x + iy)
b = 1/√2(x - iy)
Consider a basis {x, y} and alternate basis {a, b} where:
a = 1/√2(x + iy)
b = 1/√2(x - iy)
Classical method
If we assume the particle must have gone either through |x> or through |y> on its way to |b>, we sum P(a ⇒ x ⇒ b) + P(a ⇒ y ⇒ b) like bullet 3 above.
= P(a ⇒ x & x ⇒ b) + P(a ⇒ y & y ⇒ b)
= P(a⇒x)P(x⇒b) + P(a⇒y)P(y⇒b)
= 0.5*0.5 + 0.5*0.5
= 0.5
This is just classical probability theory. It turns out that if we do try to detect which way the particle went (i.e., measure it in the x-y basis, followed by the a-b basis), we find it ends up in |b> half the time.
But QM predicts that |a> should never be measured as |b>, because they're orthogonal. What went wrong is that we cannot assume that it went through either |x> or |y>.
Quantum method
Instead, we should simply take the inner product of |a> and |b>, i.e. <a|b>. We know it's zero (they're orthogonal), but we can calculate this explicitly in the x-y basis:|a> = 1/√2(1, i)
|b> = 1/√2(1, -i)
<a|b> = 1/√2 (1 * 1 + -i * -i ) = 1/√2 (1 - 1) = 0
The terms in the above sum are the terms in Feynman's (2). We could have also written this as
<a|b>
= <a|x><x|b> + <a|y><y|b>
= (1/√2)(1/√2) + (-i/√2)(-i/√2)
= ½ + -½
= 0
Where i takes on the basis vectors under consideration (in this case, x and y), and:
ψ*i = <ψ|i>
φi = <i|φ>
If you compare the two calculations (for the classical, or "which-way" case, vs the quantum case), you'll notice that they differ by some terms that we can call "interference terms." There's nothing really interfering here, unless we force ourselves to think of |a> and |b> in terms of the x-y basis, in which case we can understand this as the |x> and |y> components interfering.
Elsewhere I've demonstrated why entangling a state |x> + |y> (so that it results in |x>|0> + |y>|1>), results in a similar loss of interference (and I give a quick rehash at the bottom).
Anyway, that was all a prelude to the main course: what's happening in the two-slit experiment?
Mapping back onto the two-slit experiment
The solution to the Schrodinger equation for a plane wave isIgnoring the time component, we see that it's basically a complex number whose phase is proportional to r, which is the distance from the source. In our case we're actually close to the source, and the light's strength will be proportional to the inverse of the distance squared.
(One super confusing thing is that in some contexts, the whole Ae^(i*t) is called the "complex amplitude," but in other contexts, we call just A the amplitude. Let's not do the second. Another super confusing thing is that often when referring to the "phase" of a photon, we're talking about the relative phase of the polarization components.)
For any given point on the screen, we will have one such complex amplitude for each slit. Per Feynman's (2), we can just sum these to get the overall amplitude that will give us the probability of finding a photon at that point.
It's hard to get an intuition for what this sum looks like without pictures, but basically you're getting two complex numbers that are sometimes "in phase" (i.e., sum to a number whose modulus is bigger) and sometimes "out of phase" (mostly or entirely cancel). The overall pattern is the one you've seen before:
If we know which way the particle went, we use (3). It's hard to say the "reason" that we use that formula, but again, if we look at knowing which-way as just an entanglement rather than a "collapse" (thereby preserving the quantum nature), it turns out that equation (2) does just reduce to equation (3).
Why does entanglement cause decoherence, i.e., kill interference?
In brief, it works like this. Let's rewrite:|a> = |x> + |y>
|b> = |x> - |y>
Suppose Pb is the projector onto state |b>, which gives us the probability that some state is measured as |b>. Notice that Pb(|a>) = 0-vector. But now let's entangle it:
|a'> = |x>|x> + |y>|y>
To find the probability that |a'> ends up in |b>, we can't use Pb (since it operates on C2, whereas we now need a projector on C2⊗C2). Instead, we use Pb' = Pb ⊗ I.
If you look at the action of Pb' on |a'>, you will discover that it is not the zero-vector, but instead
√2/4 (|x> - |y>)⊗(|x> - |y>)
whose norm-squared is 0.5, just like we saw in the classical case above.
Another way of seeing this is simply writing |a'> in the a-b basis, and noticing that half of it is in |a> and the other half in |b>:
|a'> = (|a> + |b>)(|x>) + (|a> - |b>)(|y>)
= (|a>)(|x> + |y>) + (|b>)(|x> - |y>)
= |a>|a> + |b>|b>
Whew.

No comments:
Post a Comment